Embeddings explained
Intuition
Every presentation starts with a cat

If I show you one, what do you see?
- has fur
- black eyes
- two ears
- sits
-
looks away from the camera
- small
- mamal
- likes to cuddle
- eats mice …
Maths embeddings
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup. (wikipedia)
…. (!)
In IT we say it’s a mapping (form A to B)
Embeddings as expansions
The first use-case (and arguably the most common one) is expanding an element into some semantic values (latent variables).
Word embeddings
We will try to attach for each word, a “meaning” (a semantic context). We interpret “context” as whatever words are, before (or after our target word). So we will get a dataset that parses free text, and slides a window of a certain size over the full text.
In this example we’re going to use:
- 3 words sized window, 1 word prediction
ETL.. get the data, process it and load it in a specific format
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
from scipy import io
from keras.utils.np_utils import to_categorical
mat = io.loadmat("./data/word-embeddings.mat")
data = mat['data']['trainData'][0][0] - 1 # in octave arrays start from one
vocab = np.array([element[0] for element in mat['data']['vocab'][0][0].reshape(250)])
inputs = data[:3, :].T
label_index = data[3, :]
labels = to_categorical(label_index)
Printing some examples, to get a feel of what we are working with
first = 10
list(zip(
[[vocab[i] for i in words] for words in inputs[:first]],
[vocab[l] for l in label_index[:first]]
))
[([u'going', u'to', u'be'], u'.'),
([u'were', u'not', u'the'], u'first'),
([u'can', u'do', u'for'], u'each'),
([u'first', u'time', u'in'], u'my'),
([u'nt', u'have', u'the'], u'money'),
([u'know', u'what', u'to'], u'do'),
([u'i', u'do', u'nt'], u'do'),
([u'nt', u'do', u'that'], u'.'),
([u'what', u'do', u'you'], u'do'),
([u'know', u'is', u'we'], u'are')]
import keras
from keras.layers import Input
from keras.layers import Embedding
from keras.layers import merge, Lambda, Reshape, Dense, BatchNormalization
from keras.models import Model
from keras import backend as K
from keras.layers import Activation
from keras.regularizers import l2
inp_1 = Input(shape=(1,), dtype='int32')
inp_2 = Input(shape=(1,), dtype='int32')
inp_3 = Input(shape=(1,), dtype='int32')
lbl = Input(shape=(1,), dtype='int32')
DIMS = 5
word_emb = Embedding(input_dim=len(vocab), output_dim=(DIMS), W_regularizer=l2(0.0001))
emb_1 = word_emb(inp_1)
emb_2 = word_emb(inp_2)
emb_3 = word_emb(inp_3)
out = Reshape((-1,))(merge([emb_1, emb_2, emb_3], mode='concat'))
out = Dense(output_dim=len(vocab), activation='softmax')(out)
word_model = Model(input=[inp_1, inp_2, inp_3], output=out)
word_model.compile(optimizer='adam', loss='categorical_crossentropy')
word_model.summary()
____________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
====================================================================================================
input_1 (InputLayer) (None, 1) 0
____________________________________________________________________________________________________
input_2 (InputLayer) (None, 1) 0
____________________________________________________________________________________________________
input_3 (InputLayer) (None, 1) 0
____________________________________________________________________________________________________
embedding_1 (Embedding) (None, 1, 5) 1250 input_1[0][0]
input_2[0][0]
input_3[0][0]
____________________________________________________________________________________________________
merge_1 (Merge) (None, 1, 15) 0 embedding_1[0][0]
embedding_1[1][0]
embedding_1[2][0]
____________________________________________________________________________________________________
reshape_1 (Reshape) (None, 15) 0 merge_1[0][0]
____________________________________________________________________________________________________
dense_1 (Dense) (None, 250) 4000 reshape_1[0][0]
====================================================================================================
Total params: 5,250
Trainable params: 5,250
Non-trainable params: 0
____________________________________________________________________________________________________
word_model.fit([inputs[:, 0], inputs[:, 1], inputs[:, 2]], labels)
Epoch 1/10
372550/372550 [==============================] - 37s - loss: 3.6846
Epoch 2/10
372550/372550 [==============================] - 37s - loss: 3.3462
Epoch 3/10
372550/372550 [==============================] - 35s - loss: 3.2946
Epoch 4/10
372550/372550 [==============================] - 34s - loss: 3.2680
Epoch 5/10
372550/372550 [==============================] - 34s - loss: 3.2508
Epoch 6/10
372550/372550 [==============================] - 36s - loss: 3.2389
Epoch 7/10
372550/372550 [==============================] - 38s - loss: 3.2302
Epoch 8/10
372550/372550 [==============================] - 38s - loss: 3.2232
Epoch 9/10
372550/372550 [==============================] - 39s - loss: 3.2177
Epoch 10/10
372550/372550 [==============================] - 39s - loss: 3.2130
Building a reversible dictionary
vocab2id = {word: id for id, word in enumerate(vocab)}
assert vocab[vocab2id['going']] == 'going'
Getting the actuall embeddings
embeddings = word_emb.get_weights()[0]
What are the words that are the most similar to one another?
from scipy.spatial.distance import cosine
word = 'going'
def most_similar_words(word):
t_id = vocab2id[word]
t_emb = embeddings[t_id]
return [vocab[id] for id in np.argsort([cosine(t_emb, w_emb) for w_emb in embeddings])[:10]]
most_similar_words('war')
[u'war',
u'country',
u'season',
u'business',
u'game',
u'house',
u'here',
u'music',
u'company',
u'office']
Word2Vec, Glove
In NLP, the above is just the first thing that you usually do before you want to process text (i.e. substituting words with their embeddings).
Fortunately, there were many attempts (and many companies) that trained word embeddings on large corpus-es (and their expense) but made available the results.
Examples of public word embeddings libraries:
The most famous one, word2vec has the following two strategies used to training the embeddings:
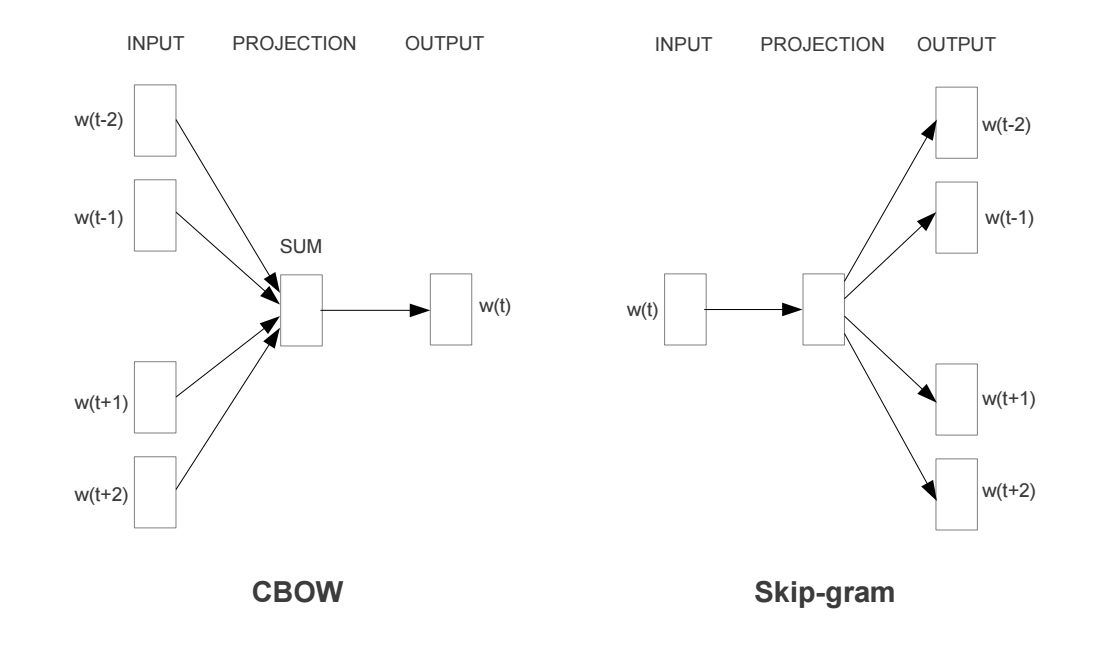
(Continuous Bag of Words), (Skip Gram model)
These embeddings have some pretty cool properties:

One downside of embeddings is that they are specific to what they have been trained on. In this case, English word embeddings are specific, to English and don’t relate in any way to embeddings of other languages (except for the fact that distances between equivalent words should have roughly the same values)
Same space aligned embeddings
You can also have embeddings aligned in the same vector space
FastText embeddings have a git repo that you can use to align all the 190 language embeddings on the same vector space.
One thing that you can use them for is to do a quick, dirty and imperfect translation mechanism, where for each word in language A, you take it’s embeddings, and search the closest embedding form language B. Having found that embedding you can now substitute it with the word it stands for.
Bellow is a translation done using this mechanism.
acesta este un text frumos scris
lui est un texte plaisant écrit
Elemental embeddings
Another use-case for embeddings is expanding your own elements into a “semantic” representation.
We will be using a wine-selection dataset hosted on Kaggle.
import pandas as pd
from IPython.display import display
table = pd.read_json('./winemag-data-130k-v2.json', encoding = "ISO-8859-1")
display(table.head())
| country | description | designation | points | price | province | region_1 | region_2 | taster_name | taster_twitter_handle | title | variety | winery | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Italy | Aromas include tropical fruit, broom, brimston... | Vulkà Bianco | 87 | NaN | Sicily & Sardinia | Etna | None | Kerin O’Keefe | @kerinokeefe | Nicosia 2013 Vulkà Bianco (Etna) | White Blend | Nicosia |
| 1 | Portugal | This is ripe and fruity, a wine that is smooth... | Avidagos | 87 | 15.0 | Douro | None | None | Roger Voss | @vossroger | Quinta dos Avidagos 2011 Avidagos Red (Douro) | Portuguese Red | Quinta dos Avidagos |
| 2 | US | Tart and snappy, the flavors of lime flesh and... | None | 87 | 14.0 | Oregon | Willamette Valley | Willamette Valley | Paul Gregutt | @paulgwine | Rainstorm 2013 Pinot Gris (Willamette Valley) | Pinot Gris | Rainstorm |
| 3 | US | Pineapple rind, lemon pith and orange blossom ... | Reserve Late Harvest | 87 | 13.0 | Michigan | Lake Michigan Shore | None | Alexander Peartree | None | St. Julian 2013 Reserve Late Harvest Riesling ... | Riesling | St. Julian |
| 4 | US | Much like the regular bottling from 2012, this... | Vintner's Reserve Wild Child Block | 87 | 65.0 | Oregon | Willamette Valley | Willamette Valley | Paul Gregutt | @paulgwine | Sweet Cheeks 2012 Vintner's Reserve Wild Child... | Pinot Noir | Sweet Cheeks |
We’re only going to take ‘taster_name’, ‘variety’ and ‘country’ fields into account.
def count_unique(column_name):
return len(table[column_name].unique())
count_unique('taster_name'), count_unique('variety'), count_unique('country')
(20, 708, 44)
See that we have values for all the point rows
import numpy as np
sum(np.isnan(table['points'].values))
0
table['taster_name'].unique()
array([u'Kerin O\u2019Keefe', u'Roger Voss', u'Paul Gregutt',
u'Alexander Peartree', u'Michael Schachner', u'Anna Lee C. Iijima',
u'Virginie Boone', u'Matt Kettmann', None, u'Sean P. Sullivan',
u'Jim Gordon', u'Joe Czerwinski', u'Anne Krebiehl\xa0MW',
u'Lauren Buzzeo', u'Mike DeSimone', u'Jeff Jenssen',
u'Susan Kostrzewa', u'Carrie Dykes', u'Fiona Adams',
u'Christina Pickard'], dtype=object)
Let’s make some reversible dictionaries so we can restore the strings from ids and vice-versa
taster2id = {taster: id for id, taster in enumerate(table['taster_name'].unique())}
id2taster = {id: taster for id, taster in enumerate(table['taster_name'].unique())}
variety2id = {taster: id for id, taster in enumerate(table['variety'].unique())}
id2variety = {id: taster for id, taster in enumerate(table['variety'].unique())}
country2id = {taster: id for id, taster in enumerate(table['country'].unique())}
id2country = {id: taster for id, taster in enumerate(table['country'].unique())}
Compiling a dataset that has only the above values and uses ‘points’ as labels
data = np.array([[taster2id[t], variety2id[v], country2id[c]] for t, v, c in table[['taster_name', 'variety', 'country']].values])
labels = table[['points']].values
assert data.shape[0] == labels.shape[0]
# print some examples
list(zip(data[5:10], labels[5:10]))
[(array([4, 5, 3]), array([87])),
(array([0, 6, 0]), array([87])),
(array([1, 7, 4]), array([87])),
(array([5, 7, 5]), array([87])),
(array([1, 2, 4]), array([87]))]
The embeddings model just translates the element ids into embedded values. We dot product all the permutation and expect that their sum is equal to the predicted price.
We also add some bias terms to account for the specific ‘biases’ of each element.
import keras
from keras.layers import Input
from keras.layers import Embedding
from keras.layers import merge, Lambda, Reshape, Dense, BatchNormalization
from keras.models import Model
from keras import backend as K
from keras.layers import Activation
from keras.regularizers import l2
nam_inp = Input(shape=(1,), dtype='int32')
var_inp = Input(shape=(1,), dtype='int32')
cty_inp = Input(shape=(1,), dtype='int32')
DIMS = 10
lbl = Input(shape=(1,), dtype='int32')
nam_emb = Embedding(input_dim=len(taster2id), output_dim=(DIMS), W_regularizer=l2(0.0001))
nam_bis = Embedding(input_dim=len(taster2id), output_dim=1, init='zero')
var_emb = Embedding(input_dim=len(variety2id), output_dim=(DIMS), W_regularizer=l2(0.0001))
var_bis = Embedding(input_dim=len(variety2id), output_dim=1, init='zero')
cty_emb = Embedding(input_dim=len(country2id), output_dim=(DIMS), W_regularizer=l2(0.0001))
cty_bis = Embedding(input_dim=len(country2id), output_dim=1, init='zero')
nam_rsh = BatchNormalization(axis=1)(Reshape((-1, 1))(nam_emb(nam_inp)))
var_rsh = BatchNormalization(axis=1)(Reshape((-1, 1))(var_emb(var_inp)))
cty_rsh = BatchNormalization(axis=1)(Reshape((-1, 1))(cty_emb(cty_inp)))
dot1 = merge([nam_rsh, var_rsh], mode='dot', dot_axes=1)
dot2 = merge([nam_rsh, cty_rsh], mode='dot', dot_axes=1)
dot3 = merge([var_rsh, cty_rsh], mode='dot', dot_axes=1)
dot = merge([dot1, dot2, dot3], mode='sum')
dot = merge([dot, nam_bis(nam_inp)], mode='sum')
dot = merge([dot, var_bis(var_inp)], mode='sum')
dot = merge([dot, cty_bis(cty_inp)], mode='sum')
dot = Reshape((1,))(dot)
out = Activation(activation='relu')(dot)
model = Model([nam_inp, var_inp, cty_inp], out)
model.summary()
model.compile(optimizer='rmsprop', loss='mae')
____________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
====================================================================================================
input_5 (InputLayer) (None, 1) 0
____________________________________________________________________________________________________
input_6 (InputLayer) (None, 1) 0
____________________________________________________________________________________________________
input_7 (InputLayer) (None, 1) 0
____________________________________________________________________________________________________
embedding_2 (Embedding) (None, 1, 10) 200 input_5[0][0]
____________________________________________________________________________________________________
embedding_4 (Embedding) (None, 1, 10) 7080 input_6[0][0]
____________________________________________________________________________________________________
embedding_6 (Embedding) (None, 1, 10) 440 input_7[0][0]
____________________________________________________________________________________________________
reshape_2 (Reshape) (None, 10, 1) 0 embedding_2[0][0]
____________________________________________________________________________________________________
reshape_3 (Reshape) (None, 10, 1) 0 embedding_4[0][0]
____________________________________________________________________________________________________
reshape_4 (Reshape) (None, 10, 1) 0 embedding_6[0][0]
____________________________________________________________________________________________________
batchnormalization_1 (BatchNorma (None, 10, 1) 40 reshape_2[0][0]
____________________________________________________________________________________________________
batchnormalization_2 (BatchNorma (None, 10, 1) 40 reshape_3[0][0]
____________________________________________________________________________________________________
batchnormalization_3 (BatchNorma (None, 10, 1) 40 reshape_4[0][0]
____________________________________________________________________________________________________
merge_2 (Merge) (None, 1, 1) 0 batchnormalization_1[0][0]
batchnormalization_2[0][0]
____________________________________________________________________________________________________
merge_3 (Merge) (None, 1, 1) 0 batchnormalization_1[0][0]
batchnormalization_3[0][0]
____________________________________________________________________________________________________
merge_4 (Merge) (None, 1, 1) 0 batchnormalization_2[0][0]
batchnormalization_3[0][0]
____________________________________________________________________________________________________
merge_5 (Merge) (None, 1, 1) 0 merge_2[0][0]
merge_3[0][0]
merge_4[0][0]
____________________________________________________________________________________________________
embedding_3 (Embedding) (None, 1, 1) 20 input_5[0][0]
____________________________________________________________________________________________________
merge_6 (Merge) (None, 1, 1) 0 merge_5[0][0]
embedding_3[0][0]
____________________________________________________________________________________________________
embedding_5 (Embedding) (None, 1, 1) 708 input_6[0][0]
____________________________________________________________________________________________________
merge_7 (Merge) (None, 1, 1) 0 merge_6[0][0]
embedding_5[0][0]
____________________________________________________________________________________________________
embedding_7 (Embedding) (None, 1, 1) 44 input_7[0][0]
____________________________________________________________________________________________________
merge_8 (Merge) (None, 1, 1) 0 merge_7[0][0]
embedding_7[0][0]
____________________________________________________________________________________________________
reshape_5 (Reshape) (None, 1) 0 merge_8[0][0]
____________________________________________________________________________________________________
activation_1 (Activation) (None, 1) 0 reshape_5[0][0]
====================================================================================================
Total params: 8,612
Trainable params: 8,552
Non-trainable params: 60
____________________________________________________________________________________________________
model.fit([data[:, 0], data[:, 1], data[:, 2]], labels)
Epoch 1/10
129971/129971 [==============================] - 9s - loss: 29.1668
Epoch 2/10
129971/129971 [==============================] - 8s - loss: 9.4990
Epoch 3/10
129971/129971 [==============================] - 8s - loss: 3.8390
Epoch 4/10
129971/129971 [==============================] - 8s - loss: 2.6311
Epoch 5/10
129971/129971 [==============================] - 8s - loss: 2.4363
Epoch 6/10
129971/129971 [==============================] - 10s - loss: 2.3623
Epoch 7/10
129971/129971 [==============================] - 11s - loss: 2.3188
Epoch 8/10
129971/129971 [==============================] - 9s - loss: 2.2963
Epoch 9/10
129971/129971 [==============================] - 8s - loss: 2.2824
Epoch 10/10
129971/129971 [==============================] - 8s - loss: 2.2726
Trying to extract some meaning from the dimensions
wines = np.array(var_emb.get_weights()[0])
# 0 - being Italian
# 1 - mainstream
# 3 - red-ness
# 8 - Sauvignon / Pinot (sweetness?)
for dimension in range(DIMS):
print(dimension, [id2variety[v] for v in np.argsort(wines[:, dimension])][:5])
(0, [u'Port', u'Albari\xf1o', u'Cabernet Sauvignon', u'Malbec', u'Nebbiolo'])
(1, [u'Ros\xe9', u'Merlot', u'Cabernet Sauvignon', u'White Blend', u'Viognier'])
(2, [u'Pinot Noir', u'Chardonnay', u'Cabernet Sauvignon', u'Champagne Blend', u'Malbec'])
(3, [u'Bordeaux-style Red Blend', u'Syrah', u'Ros\xe9', u'Red Blend', u'Pinot Noir'])
(4, [u'Pinot Noir', u'Champagne Blend', u'Chardonnay', u'Ros\xe9', u'Viognier'])
(5, [u'Chenin Blanc', u'Pinot Grigio', u'Pinot Blanc', u'Tempranillo Blend', u'Rh\xf4ne-style Red Blend'])
(6, [u'Ros\xe9', u'Red Blend', u'Syrah', u'Viognier', u'Champagne Blend'])
(7, [u'Pinot Noir', u'Chardonnay', u'Ros\xe9', u'Syrah', u'Riesling'])
(8, [u'Cabernet Sauvignon', u'Pinot Blanc', u'Pinot Gris', u'Pinot Noir', u'Sauvignon Blanc'])
(9, [u'Petite Sirah', u'Meritage', u'Glera', u'Sauvignon', u'Tempranillo'])
name_embeddings = np.array(nam_emb.get_weights()[0])
print(" ".join(["%.2f\t" % val for val in name_embeddings[0]]))
print(" ".join(["%.2f\t" % val for val in name_embeddings[10]]))
# list(name_embeddings[0]), list(name_embeddings[10])
0.22 0.16 0.23 -0.07 -0.16 -0.33 -0.35 -0.20 0.07 -0.02
0.12 0.03 0.21 -0.29 0.19 0.11 -0.27 0.01 -0.21 -0.22
From all the examples we gave, observe the pattern?
We usually use embeddings when we want to reason about ids.
Composite (event) embeddings
Go to previous talk
If you train names as above, you’re going to be able to do additive operations on the embeddings.
We’ve trained a model to derive name embeddings that we latter used to assemble “event embeddings”.
These can be used as indexes in a database (similar elements being close to one another).
The interesting thing about embeddings right now is that we can also use them to make intelligent “Google-like” queries:
- “Air force” + “New York” + “Bombings” + “1980” -> “John Malcom”
- [note: the above is just a made-up example]
Sparse matrices to embeddings
Another example of embeddings usage is the case where we want to take a really large / sparse matrix and convert it to a reduced set value.
Arguably, Word2Vec has been shown to do exactly this (build the concurrence matrix and factor it down into a low-dimensional representation).
PCA
Just to exemplify how this might work, we’re going to take the iris dataset and use it to derive embeddings for each element.
Some ETL..
from sklearn.decomposition import PCA
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
pca = PCA(n_components=3)
pca.fit(X)
X_ = pca.transform(X)
X_[:10]
array([[-2.68420713, 0.32660731, -0.02151184],
[-2.71539062, -0.16955685, -0.20352143],
[-2.88981954, -0.13734561, 0.02470924],
[-2.7464372 , -0.31112432, 0.03767198],
[-2.72859298, 0.33392456, 0.0962297 ],
[-2.27989736, 0.74778271, 0.17432562],
[-2.82089068, -0.08210451, 0.26425109],
[-2.62648199, 0.17040535, -0.01580151],
[-2.88795857, -0.57079803, 0.02733541],
[-2.67384469, -0.1066917 , -0.1915333 ]])
Let’s how each element decomposed on only three dimensions.
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(1, figsize=(4, 3))
plt.clf()
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
plt.cla()
for name, label in [('Setosa', 0), ('Versicolour', 1), ('Virginica', 2)]:
ax.text3D(X[y == label, 0].mean(),
X[y == label, 1].mean() + 1.5,
X[y == label, 2].mean(), name,
horizontalalignment='center',
bbox=dict(alpha=.5, edgecolor='w', facecolor='w'))
# Reorder the labels to have colors matching the cluster results
y = np.choose(y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap=plt.cm.nipy_spectral,
edgecolor='k')
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
plt.show()

Auto-encoders
We can also create embeddings for multidimensional data using auto-encoders.
Auto-encoders model the function f, where f(x) = x
Auto-encoders have a “bottleneck” part where data is reduced to a low dimensional representation and then expanded back into the same dimension as the one we’ve started from.
The “bottleneck” output will be our encoding.
We’re going to use the MNIST dataset as well, to model what we’ve just said.
ETL… again
from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
X = np.expand_dims(x_train, -1)
print(X.shape)
X_val = np.expand_dims(x_test, -1)
from keras.utils.np_utils import to_categorical
y = to_categorical(y_train)
y_val = to_categorical(y_test)
(60000, 28, 28, 1)
# Data shape
print(x_train.shape)
# show raw pixels
plt.imshow(x_train[0], cmap='gray')
# plot the first 10 images
plots(x_train[:10], titles=y_train[:10])
(60000, 28, 28)


The model that we are going to create will look as follows
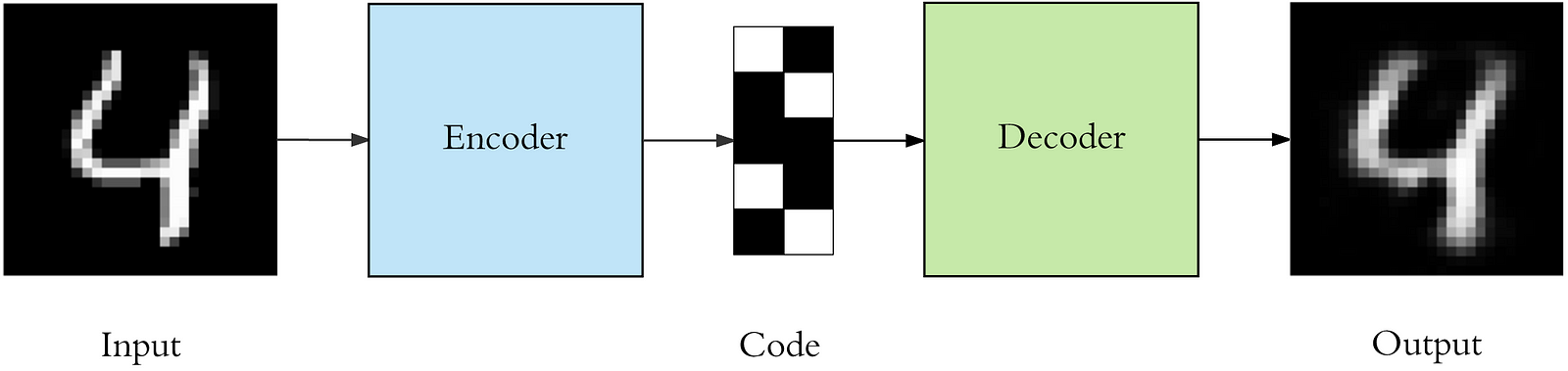
from keras.layers import Input, Dense, Convolution2D, MaxPooling2D, UpSampling2D
from keras.models import Model
input_img = Input(shape=(28, 28, 1))
# -----------
# The encoder
# -----------
x = Convolution2D(16, 3, 3, activation='relu', border_mode='same')(input_img)
x = MaxPooling2D((2, 2), border_mode='same')(x)
x = Convolution2D(8, 3, 3, activation='relu', border_mode='same')(x)
x = MaxPooling2D((2, 2), border_mode='same')(x)
x = Convolution2D(8, 3, 3, activation='relu', border_mode='same')(x)
encoded = MaxPooling2D((2, 2), border_mode='same')(x)
# at this point the representation is (4, 4, 8) i.e. 128-dimensional
# -----------
# The decoder
# -----------
x = Convolution2D(8, 3, 3, activation='relu', border_mode='same')(encoded)
x = UpSampling2D((2, 2))(x)
x = Convolution2D(8, 3, 3, activation='relu', border_mode='same')(x)
x = UpSampling2D((2, 2))(x)
x = Convolution2D(16, 3, 3, activation='relu')(x)
x = UpSampling2D((2, 2))(x)
decoded = Convolution2D(1, 3, 3, activation='sigmoid', border_mode='same')(x)
autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adadelta', loss='mae')
autoencoder.summary()
____________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
====================================================================================================
input_24 (InputLayer) (None, 28, 28, 1) 0
____________________________________________________________________________________________________
convolution2d_47 (Convolution2D) (None, 28, 28, 16) 160 input_24[0][0]
____________________________________________________________________________________________________
maxpooling2d_22 (MaxPooling2D) (None, 14, 14, 16) 0 convolution2d_47[0][0]
____________________________________________________________________________________________________
convolution2d_48 (Convolution2D) (None, 14, 14, 8) 1160 maxpooling2d_22[0][0]
____________________________________________________________________________________________________
maxpooling2d_23 (MaxPooling2D) (None, 7, 7, 8) 0 convolution2d_48[0][0]
____________________________________________________________________________________________________
convolution2d_49 (Convolution2D) (None, 7, 7, 8) 584 maxpooling2d_23[0][0]
____________________________________________________________________________________________________
maxpooling2d_24 (MaxPooling2D) (None, 4, 4, 8) 0 convolution2d_49[0][0]
____________________________________________________________________________________________________
convolution2d_50 (Convolution2D) (None, 4, 4, 8) 584 maxpooling2d_24[0][0]
____________________________________________________________________________________________________
upsampling2d_19 (UpSampling2D) (None, 8, 8, 8) 0 convolution2d_50[0][0]
____________________________________________________________________________________________________
convolution2d_51 (Convolution2D) (None, 8, 8, 8) 584 upsampling2d_19[0][0]
____________________________________________________________________________________________________
upsampling2d_20 (UpSampling2D) (None, 16, 16, 8) 0 convolution2d_51[0][0]
____________________________________________________________________________________________________
convolution2d_52 (Convolution2D) (None, 14, 14, 16) 1168 upsampling2d_20[0][0]
____________________________________________________________________________________________________
upsampling2d_21 (UpSampling2D) (None, 28, 28, 16) 0 convolution2d_52[0][0]
____________________________________________________________________________________________________
convolution2d_53 (Convolution2D) (None, 28, 28, 1) 145 upsampling2d_21[0][0]
====================================================================================================
Total params: 4,385
Trainable params: 4,385
Non-trainable params: 0
____________________________________________________________________________________________________
autoencoder.fit(X, X,
nb_epoch=10,
batch_size=256,
shuffle=True,
validation_data=(X_val, X_val))
Train on 60000 samples, validate on 10000 samples
Epoch 1/3
60000/60000 [==============================] - 79s - loss: 23.6325 - val_loss: 32.9488
Epoch 2/3
60000/60000 [==============================] - 79s - loss: 22.6607 - val_loss: 31.4966
Epoch 3/3
60000/60000 [==============================] - 81s - loss: 21.0491 - val_loss: 30.7882
Let’s see the reconstruction of a single example
plots(autoencoder.predict(np.array([X[0]])))


encoder = Model(input_img, encoded)
encoder.predict(X[:1])[0].shape
(4, 4, 8)
In the end, the “embeddings” will can be mapped like this.
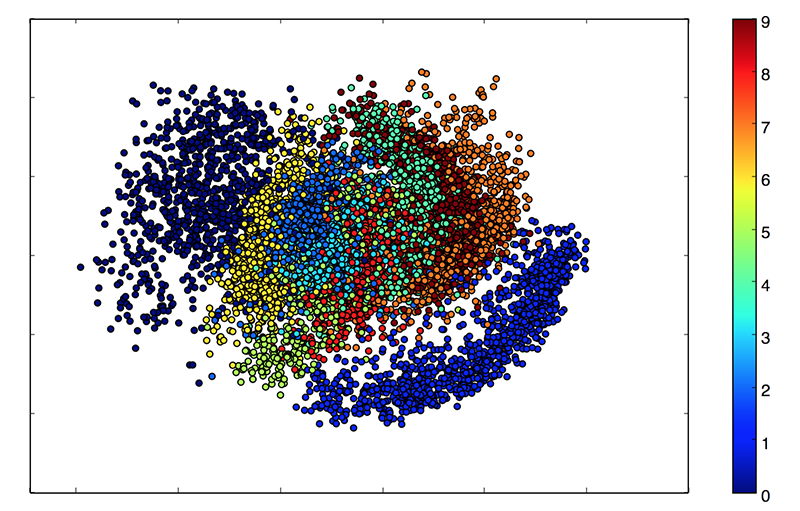
def plots(ims, figsize=(12, 6), rows=1, interp=False, titles=None, display=False):
if type(ims[0]) is np.ndarray:
ims = np.array(ims).astype(np.uint8)
if len(ims.shape) != 3:
# Find out if the last dimension is not the color channel.
# If we have K.dim_ordering('th') then the color channel is the second dimension
# The code bellow ensures the images are in the K.dim_ordering('tf') format (channels last)
if (ims.shape[-1] not in {1, 3}):
# Take the color axis(1) and put it at the back(4)
ims = ims.transpose((0, 2, 3, 1))
else:
# We have no color information, so no need to change the dimensions to put color on the back
pass
f = plt.figure(figsize=figsize)
for i in range(len(ims)):
sp = f.add_subplot(rows, len(ims) // rows, i + 1)
sp.axis('Off')
if titles is not None:
sp.set_title(titles[i], fontsize=16)
if ims.shape[-1] == 1:
# Last axis is a single color channel so we can discard it and treat the data as a gray image
plt.imshow(np.squeeze(ims[i]), interpolation=None if interp else 'none', cmap='gray')
else:
plt.imshow(ims[i], interpolation=None if interp else 'none')
if display:
return f
Conclusions
- IDs always mean embeddings!
- NLP stands on the shoulders of word2vec, glove, fasttext
- Usually, embeddings are additive

Comments